數控機床傳動系統精度可靠性研究
0 引言
經典機械精度設計理論把各個誤差項看成是確定的量,現代機械精度設計理論認為各個誤差項在隨機因素的影響下是隨機量。經典機械可靠性設計理論主要是對機械部件的疲勞強度可靠性進行設計,現代機械可靠性設計理論已經滲透到機械精度可靠性設計中,機械精度可靠性設計是機械可靠性設計的重要方面。文獻研究了不完全概率信息下牛頭刨床主運動機構運動精度可靠性穩健設計問題。文獻以2K-V型減速機為研究對象,綜合考慮系統中各零件的加工誤差、安裝誤差、間隙及其齒輪嚙合剛度、軸承剛度等因素對傳動精度產生的影響,建立了該系統的動態傳動精度非線性動力學計算模型。文獻提供了一種少齒數齒輪傳動系統輸出運動誤差的數值計算方法。文獻分別用矩陣法和作用線增量法建立了機構運動精度誤差分析模型。文獻對機構運動精度可靠性優化設計題進行了初步探索。文獻在運動學的范疇內,探討了運動副間隙對機構運動輸出精度的影響。文獻考慮徑向跳動、軸向跳動和齒距累積誤差的影響,推導出了傳動鏈線性誤差公式。文獻建立了基于模糊數的機械精度模糊可靠性的基本模型。
上述文獻沒有把精度設計理論和可靠性設計理論結合起來對齒輪傳動精度進行研究,并且沒有考慮多因素綜合作用下齒輪傳動機構的傳動精度可靠性。本文結合機械精度設計理論和機械可靠性設計理論,首次建立多因素綜合作用下的數控機床進給傳動系統精度可靠性模型,并計算出多因素作用下進給傳動系統傳動精度可靠度,利用靈敏度設計理論對影響傳動精度因素的重要度進行排序,找出精度可靠性的薄弱環節,提出提高進給傳動系統精度可靠性的措施,并將其應用在某數控重型臥式車床進給傳動系統的精度可靠性設計中。該研究方法對解決其他精度可靠性設計問題同樣具有參考價值。
1 傳動精度的概念
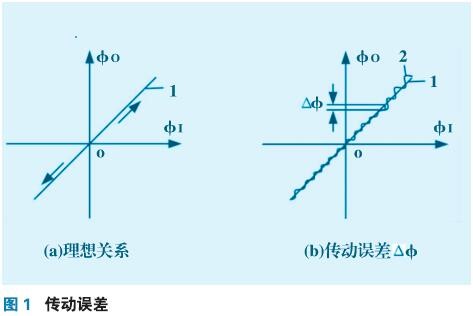
當i=1時,φi與φo之間的關系曲線如圖1a中的直線1所示。在實際傳動過程中輸出軸的轉角總會存在誤差。圖1b中,曲線2表示單向回轉時,由于存在轉角誤差Δφ,輸出軸轉角φo與輸入軸轉角φi之間的關系。
轉角誤差Δφ與其在分度圓上的線性誤差Δ之間有如下關系:
2 進給傳動系統精度可靠性模型
2.1 精度可靠度基本概念
產品在規定的加工、測量和裝配條件下,其實際精度滿足設計要求的概率稱為產品精度的可靠度。假定產品的實際精度用b表示,其設計精度為[b]。考慮加工、測量、裝配的隨機因素,其實際精度滿足[b]的要求為一隨機事件A,則產品精度的可靠度為
2.2 精度可靠性數學模型
齒輪傳動過程中,影響齒輪傳動誤差的因素主要是齒輪本身的加工誤差,以及齒輪的裝配偏心等誤差。影響齒輪傳動裝置傳動精度的主要因素除齒輪本身的誤差因素外,還有中心距偏差、傳動軸彈性變形及溫度變化等。由上可知,齒輪傳動裝置或傳動鏈的傳動誤差是由齒輪的制造誤差和安裝誤差造成的,是傳動鏈中齒輪本身、所在軸和軸承等零部件制造裝配時誤差的綜合作用的結果。
2.2.1 傳動誤差精度可靠性模型
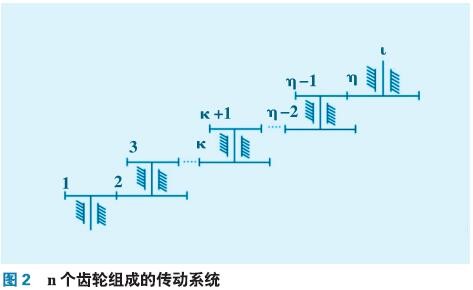
在綜合考慮切向綜合誤差(幾何偏心、運動偏心、基節偏差、齒廓偏差)、齒距累積誤差、齒輪徑向跳動、公法線長度變動、軸的徑向跳動、齒輪與軸的配合間隙、滾動軸承內外圈徑向跳動因素的作用下,假設各個誤差項都符合正態分布,建立的一對齒輪的傳動誤差的均值μ1,2和標準差σ1,2的數學模型如下:
式中,F′i1、F′i2分別為齒輪1、2的切向綜合誤差,μm;Fp1、Fp2分別為齒輪1、2的齒距累積誤差,μm;Fr1、Fr2分別為齒輪1、2的徑向跳動公差,μm;Fw1、Fw2分別為齒輪1、2的公法線長度變動公差,μm;s1、s2分別為軸1、2的徑向跳動公差,μm;C1、C2分別為齒輪與軸的配合間隙公差,μm;U1、U2分別為滾動軸承內外滾道徑向跳動公差,μm;z2為從動輪2的齒數;mn為齒輪的法面模數,mm。
2.2.2 齒輪傳動誤差的統計計算式
齒輪傳動系統傳動誤差的綜合式為
式中,μφl為齒輪傳動系統傳動誤差折算到輸出軸l上的傳動誤差的均值;σφl為齒輪傳動系統傳動誤差折算到輸出軸l上的傳動誤差的標準差;σK-1,K為第K-1與第K個齒輪折算到第K個齒輪所在軸上的傳動誤差的標準差。
2.2.3 齒輪機構傳動誤差可靠度計算
式中,F(x)為傳動誤差的正態分布函數;φ(x)為傳動誤差標準正態分布函數。
3 某重型車床精度可靠性分析
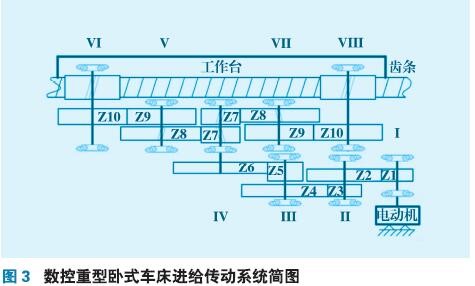
某數控重型臥式車床的進給傳動系統結構簡圖見圖3,圖中,Zi是齒輪i的編號。運動由Ⅰ軸輸入,經過Ⅱ軸、Ⅲ軸到達Ⅳ軸,傳動系統在Ⅳ軸被分成兩個分支,分別是Ⅳ-Ⅴ-Ⅵ和Ⅳ-Ⅶ-Ⅷ,Ⅳ軸和Ⅴ軸、Ⅳ軸和Ⅶ軸之間分別采用斜齒輪液壓消隙機構使輸出軸Ⅵ軸、Ⅷ軸向兩側壓緊,達到消除間隙的目的。
該數控重型臥式車床的定位精度要求是[-0.01mm,0.01mm],但是由于該車床的工作負載大,進給傳動系統的傳動精度隨著時間的推移會不斷下降,精度保持性、精度可靠性不高,本文通過理論分析,完成以下工作:
3.1 結構改進前的精度可靠性分析
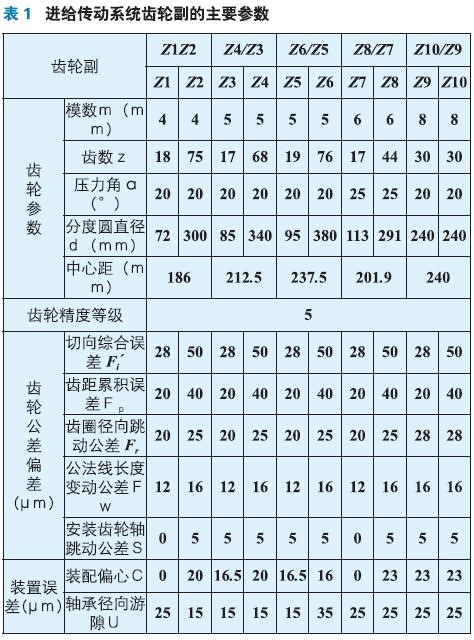
該數控重型臥式車床進給傳動系統齒輪副的主要參數如表1所示。
利用式(5)所示的數學模型,分別求出每一級齒輪的傳動誤差折算到從動輪所在軸上的傳動誤差的標準差,計算結果如下:
3.2 理論分析結果與實驗結果的對比
利用雙頻激光干涉儀,按照標準Gb/T17421.2
由分析結果可知,此齒輪進給傳動系統的精度可靠度不高,主要是由于該進給傳動系統的設計采用經驗與類比的設計方法,經驗類比設計方法存在很多缺陷與不足。
3.3 結果分析與改進措施
3.3.1 輸入輸出軸精度可靠性薄弱環節分析
改進措施:對于該數控重型臥式車床的進給傳動系統,可降低輸入軸上齒輪副精度,提高輸出軸上齒輪副精度。
3.3.2 齒輪副精度可靠性薄弱環節分析
分析齒輪切向綜合誤差F′i、齒距累計誤差Fp、齒輪徑向跳動Fr、公法線長度變動Fw、軸的徑向跳動s、齒輪與軸的配合間隙C、滾動軸承內外圈徑向跳動U對傳動誤差的影響程度,計算考慮單一因素的齒輪傳動誤差,利用式(5),保留考慮的因素,不考慮的因素置零,計算結果如表3所示。切向綜合誤差的重要度指只考慮切向綜合誤差所計算的傳動誤差與考慮全部因素所計算的傳動誤差的比值,其他誤差項重要度的定義與此相同。
由此計算出上述7個因素對齒輪傳動精度重要度的大小,計算結果如表3所示。由表3可知,對傳動精度影響最大的因素是切向綜合誤差。切向綜合誤差是在接近齒輪的工作狀態下測量的,是幾何偏心、運動偏心、基節偏差、齒廓偏差綜合測量的結果,是評定齒輪傳動準確性的首選指標。改進措施:對于該數控重型臥式車床的進給傳動系統,應該著重減小齒輪的切向綜合誤差,這樣會明顯提高進給傳動系統的傳動精度。
3.4 結構改進后的精度可靠性分析
3.4.1 輸入輸出精度調整后精度可靠性分析
當進給傳動系統的齒輪全部采用5級精度時,齒輪進給傳動系統傳動誤差折算到輸出軸上的傳動誤差是0.49691′,此時,由式(8)計算出的進給傳動系統的精度可靠度為69.22%。當進給傳動系統的第一級齒輪采用6級精度、其余齒輪采用5級精度時,齒輪進給傳動系統傳動誤差折算到輸出軸上的傳動誤差是0.49696′,此時,由式(8)計算出的進給傳動系統的精度可靠度也是69.22%。當進給傳動系統的最后一級齒輪副采用4級精度、其余齒輪采用5級精度時,齒輪進給傳動系統傳動誤差折算到輸出軸上的傳動誤差是0.42001′,由式(8)計算出的進給傳動系統傳動誤差的可靠度為
3.4.2 齒輪誤差項調整后精度可靠性分析
僅將齒輪的切向綜合誤差提高一個精度等級時,計算出齒輪進給傳動系統傳動誤差折算到輸出軸上的誤差為σφl=0.4281′,此時計算出的該進給傳動系統的精度可靠度為r=p(-0.5067′≤Δφl≤0.5067′)=76.20%。
4 結論
Δφ=3.44Δ/r=6.88Δ/d (2)
式中,r為齒輪分度圓半徑,mm;d為齒輪分度圓直徑,mm。
R=P(A)=P(b< [b]) (3)
產品的實際精度不能滿足設計要求稱為失效,記為A,則其失效概率為
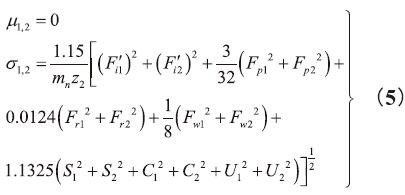
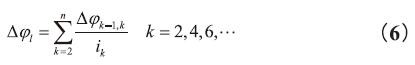
(1)對進給傳動系統進行精度可靠性建模,定量評估和預測現有進給傳動系統的實際精度滿足設計定位精度[-0.01mm,0.01mm]的可靠度。
(2)利用精度可靠性模型分析影響進給傳動系統定位精度的主要因素,對影響傳動精度因素的重要度進行排序,找出精度可靠性的薄弱環節,對薄弱環節進行改進設計,以提高整個進給傳動系統的精度可靠性。
σφ2=0.2736′,σφ4=0.2386′,σφ6=0.2334′,σφ8=0.2978′,σφ10 =0.3867′
由式(7)可知,齒輪進給傳動系統傳動誤差折算到輸出軸上的均值和標準差為
將進給傳動系統的線性定位精度[-0.01mm,0.01mm]轉化成角度定位精度為[-0.5067′,0.5067′],由式(8)可得進給傳動系統傳動精度的可靠度為
R=P(-0.5067′≤Δφl ≤0.5067′)=69.22% (10)
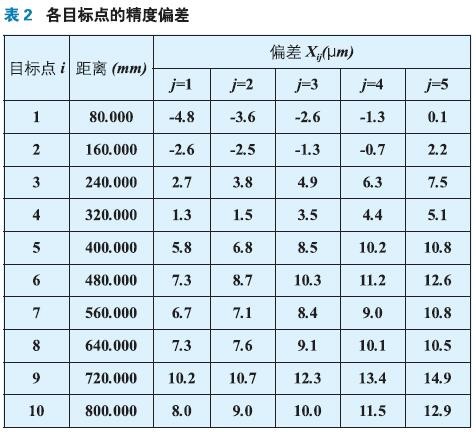
-2000(ISO 230-2:1997)對該數控重型臥式車床進行精度可靠性實驗,在工作區間內等間距地取10個目標點,每一個目標點i距初始選定點的距離及其精度偏差如表2所示(j為測量次數)。
將式(9)寫成如下形式:
σφl =σφl(σ1,2,σ3,4,σ5,6,σ7,8,σ9,10)
將其按照多元函數泰勒級數展開公式展開,省略高階項可得
σφl=3.2107×10-4σ1,2+0.0045σ3,4+0.0701σ5,6+0.5993σ7,8+0.7782σ9,10 (11)
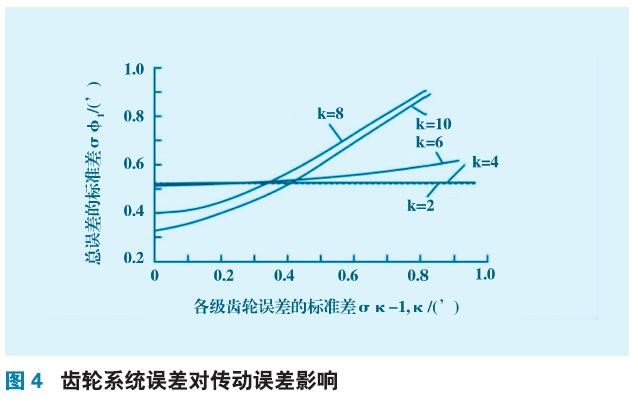
由式(11)可知,σK-1,K(K=2,4,6,8,10)的權系數越大,σK-1,K的靈敏度越高,即對進給傳動系統的傳動精度的影響越大,σK-1,K(K=2,4,6,8,與σφl的關系如圖4所示。
R=P(-0.5067′≤Δφl≤0.5067′)=76.98%
該數控重型臥式車床的進給傳動系統齒輪副不同的組合精度等級對進給傳動系統精度可靠度的影響如圖5所示,由圖5可見,輸入端齒輪精度的降低對整個進給傳動系統的定位精度的影響可以忽略,輸出端齒輪精度的升高對整個進給傳動系統的定位精度的影響很大。
(2)某數控重型臥式車床的進給傳動系統的傳動精度可靠度是69.22%,輸入軸齒輪系統精度降低一個等級,該系統的傳動精度保持不變,但是輸出軸齒輪系統精度升高一個等級,傳動精度可靠度可從69.22%提高至76.98%。
(3)齒輪副誤差因素對傳動精度的影響程度由大到小依次是齒輪切向綜合誤差、滾動軸承內外圈徑向跳動、齒輪與軸的配合間隙、齒距累積誤差、齒輪徑向跳動、公法線長度變動、軸的徑向跳動。僅將切向綜合誤差提高一個精度等級時,傳動精度可靠度可從69.22%提高至76.20%。由此可見影響傳動精度最大的因素是切向綜合誤差。
 銷售熱線:188 2384 2885
銷售熱線:188 2384 2885